LeetCode 011 盛最多水的容器

有勇气的牛排 26 算法 2025-08-08 22:11:03

程序员兼职接单交流

编程交流

进群口令：博客

题目

给定一个长度为 n 的证书数组 height。有 n 条垂线，第 i 条线的两个端点是(i, 0)和(i, height)。

找出其中的两条线，是的他们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以存储的最大水量。

说明：你不能倾斜容器。

示例 1：

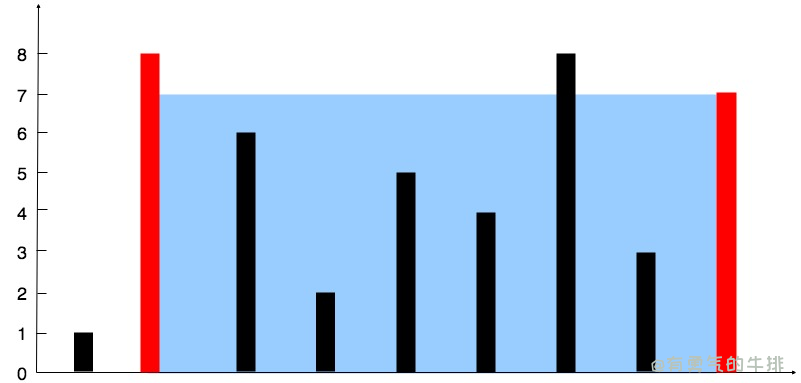
LeetCode 011 盛最多水的容器

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

n == height.length
2 <= n <= 10^5
0 <= height[i] <= 10^4

问题分析

给定数组 height，每个元素表示竖线的高度。
任意两条线与x轴可以组成一个容器。
容器容量公示：

面积 = (右边界索引 - 左边界索引) × (左边高度, 右边高度)
目标：找最大面积。

暴力解法

遍历所有可能得两条线(i, j)，计算面积。
时间复杂度：O(n²)，当 n=10⁴ 时会超时。

双指针法(推荐)

核心思想

左右两个指针分别从数组两端出发。
每次计算容器面积，并记录最大值。
然后 移动高度较小的指针，因为容量由短板决定。
- 如果一定较高的那边，宽度变小，高度不变或更低 → 不可能增大容量。
- 只有移动较小的那边，才有可能找到更高的板，增加容量。

# -*- coding: utf-8 -*-
from typing import List


class Solution:
    def maxArea(self, height: List[int]) -> int:
        left = 0
        right = len(height) - 1
        max_area = 0

        # print(f"总宽度：{right}")

        while left < right:
            # 当前宽
            width = right - left
            # 最小高度
            min_height = min(height[left], height[right])
            # 当前面积
            max_area = max(max_area, width * min_height)

            # print(f"宽度：{width}")
            # print(f"高度：{height[left], height[right], min_height}")
            # print(f"max_area：{max_area}")
            
            # 高度最小的 向内收缩
            if height[left] < height[right]:
                left += 1
            else:
                right -= 1

        return max_area


Solution().maxArea([1, 8, 6, 2, 5, 4, 8, 3, 7])
# Solution().maxArea([1, 8, 6, 2, 5])

时间复杂度：O(n)，只遍历一次。

空间复杂度：O(1)，只用常数变量。

<h2><a id="_0"></a>题目</h2> 给定一个长度为 <code>n</code> 的证书数组 <code>height</code>。有 <code>n</code> 条垂线，第 <code>i</code> 条线的两个端点是<code>(i, 0)</code>和<code>(i, height)</code>。 找出其中的两条线，是的他们与 <code>x</code> 轴共同构成的容器可以容纳最多的水。 返回容器可以存储的最大水量。 说明：你不能倾斜容器。 示例 1： <img src="https://static.couragesteak.com/article/d1191f158c5d3f019050309c982d1499.png" alt="LeetCode 011 盛最多水的容器" /> <pre><code class="lang-">输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。 </code></pre> 示例 2： <pre><code class="lang-">输入：height = [1,1] 输出：1 </code></pre> 提示： <ul> <li><code>n == height.length</code></li> <li><code>2 <= n <= 10^5</code></li> <li><code>0 <= height[i] <= 10^4</code></li> </ul> <h2><a id="_33"></a>问题分析</h2> <ul> <li> 给定数组 <code>height</code>，每个元素表示竖线的高度。 </li> <li> 任意两条线与x轴可以组成一个容器。 </li> <li> 容器容量公示： 面积 = (右边界索引 - 左边界索引) × (左边高度, 右边高度) </li> <li> 目标：找最大面积。 </li> </ul> <h2><a id="_45"></a>暴力解法</h2> <ul> <li>遍历所有可能得两条线<code>(i, j)</code>，计算面积。</li> <li>时间复杂度：O(n²)，当 n=10⁴ 时会超时。</li> </ul> <h2><a id="_50"></a>双指针法(推荐)</h2> 核心思想 <ul> <li>左右两个指针分别从数组两端出发。</li> <li>每次计算容器面积，并记录最大值。</li> <li>然后 移动高度较小的指针，因为容量由短板决定。 <ul> <li>如果一定较高的那边，宽度变小，高度不变或更低 → 不可能增大容量。</li> <li>只有移动较小的那边，才有可能找到更高的板，增加容量。</li> </ul> </li> </ul> <pre><div class="hljs"><code class="lang-python"># -*- coding: utf-8 -*- from typing import List class Solution: def maxArea(self, height: List[int]) -> int: left = 0 right = len(height) - 1 max_area = 0 # print(f"总宽度：{right}") while left < right: # 当前宽 width = right - left # 最小高度 min_height = min(height[left], height[right]) # 当前面积 max_area = max(max_area, width * min_height) # print(f"宽度：{width}") # print(f"高度：{height[left], height[right], min_height}") # print(f"max_area：{max_area}") # 高度最小的向内收缩 if height[left] < height[right]: left += 1 else: right -= 1 return max_area Solution().maxArea([1, 8, 6, 2, 5, 4, 8, 3, 7]) # Solution().maxArea([1, 8, 6, 2, 5]) </code></div></pre> 时间复杂度：O(n)，只遍历一次。 空间复杂度：O(1)，只用常数变量。

LeetCode 011 盛最多水的容器

题目

问题分析

暴力解法

双指针法(推荐)

评论区